江苏质量网欢迎您！2024年05月20日 星期一

南京雨润集团品质管理中心 陈湘来

摘要：腊肠定量包装的净含量值是一个值得探讨的重要命题。对于生产厂家来说，过程中最大的问题是实际净含量值显著的大于标准重量。本文采用六西格玛管理的DMAIC流程，通过对两个不同批次的腊肠净含量的统计分析，探讨了腊肠定量过程的最优过程均值问题，并设计出较为合理的净含量上下限范围，取得了良好的效果。

关键字：六西格玛；腊肠；定量过程；质量改进

1 引言

六西格玛管理方法是由摩托罗拉公司首创的，并将之用于产品质量的改进。在实施六西格玛管理的短短时间里，摩托罗拉公司就取得了令举世瞩目的成就：销售额增长5倍，利润几乎每年增长20%；产品的不合格率从6210PPM（约四西格玛水平）减少到32PPM（约5.5西格玛水平），实施六西格玛管理法带来的节约额累计达140亿美元，并于1988年获得了首届波里奇国家质量奖。

六西格玛管理体系虽然是由摩托罗拉公司所创立，但是，真正把这一高度有效的质量管理体系变成一种管理哲学，从而形成一种企业文化的是由杰克·韦尔奇领导下的通用电气公司。通用公司在1996年年初开始，在公司全面推行六西格玛的流程变革方法，并将六西格玛作为一种管理战略，且列在其三大公司战略举措之首。而六西格玛也逐渐从一种质量管理方法变成了一个高度有效的企业流程设计、改造和优化技术，继而成为世界上追求管理卓越性的企业最为重要的战略举措。六西格玛管理的实施，使得通用公司从一个优秀的企业蜕变为卓越的企业。六西格玛管理被杰克·韦尔奇称许为“通用所采用过的最重要的管理措施”。

越来越多的公司——不仅制造行业，而且服务行业——开始实施六西格玛，并运用六西格玛的管理思想于企业管理的各个方面^[1-4]。六西格玛管理逐渐成为企业组织追求卓越管理，在全球化、信息化的竞争环境中处于不败之地的坚实管理基础。

本文采用六西格玛管理中的DMAIC方法，对腊肠的包装净含量问题进行研究。对于腊肠定量包装，过程中最易出现的质量问题为净含量不足。为了保证包装腊肠产品不出现负偏差，人为设定的每包腊肠超包值偏大，这无形中增加了生产成本，造成了损失。本文应用六西格玛管理DMAIC流程，针对包装腊肠产品净含量偏大的问题，应用基于质量损失函数与截尾正态分布的极值求解模型^{[5, 6]}，找出包装产品定量过程的最优过程均值，并设计出合理的上下限范围。本文数据统计分析所采用的软件为MINITAB 14与MATLAB 2009^[7]，并取显著性水平为0.05。

2 定义阶段

对于腊肠定量包装过程，最容易出现问题是包装净含量不足。为了避免出现这样的问题，目前每包腊肠产品的超包值普遍较大，明显超过腊肠产品的定量标准值。显然，这是有利于消费者的。但是，这对于生产者，是否为最优设置，是一个值得讨论的命题。也就是说，对于定量腊肠产品，在销售价格一定的情况下，实际净含量越大，消费者的满意程度一般也越高；另一方面，实际净含量越大，生产成本越高。对于生产者，无论偏向哪一方，均会产生损失。应当在消费者满意程度与生产成本之间进行权衡，得到关于过程均值的一个最优设置，即腊肠定量过程的最优期望均值，从而使得总损失最小。

3 测量阶段

腊肠的标准重量为450（单位：克，下同），目前净含量的允许范围为[450, 455]。现随机抽取两个批次的腊肠作为样本，每个批次共40个样品，称其净含量，得到样本数据，如表1所示。

表1 样本数据

4 分析阶段

4.1 批次I的正态性检验

假定变量X为批次I的样本净含量，那么变量X的直方图与正态概率图分别如图1与图2所示所示。

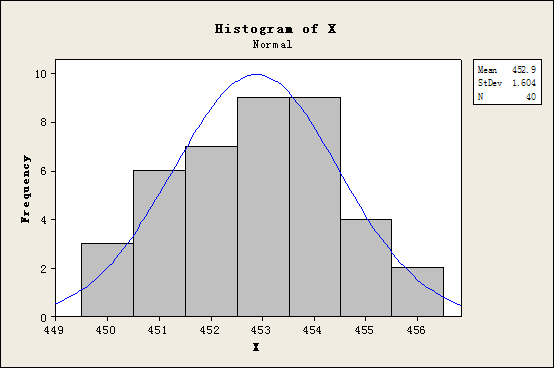
图1 变量X的直方图

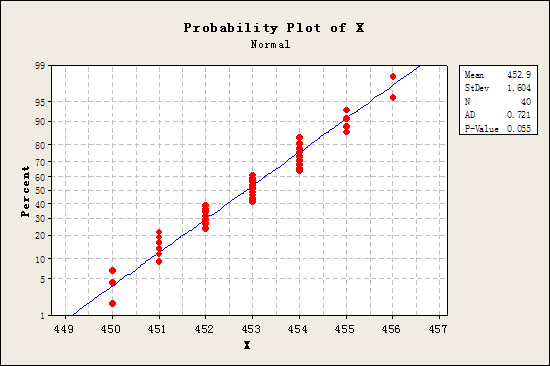
图2 变量X的正态概率图

由于图2中的P值(P-Value)大于0.05，因而可以认为变量X服从正态分布。

4.2 批次II的正态性检验

假定变量Y为批次II的样本净含量，那么变量Y的直方图与正态概率图分别如图3与图4所示所示。

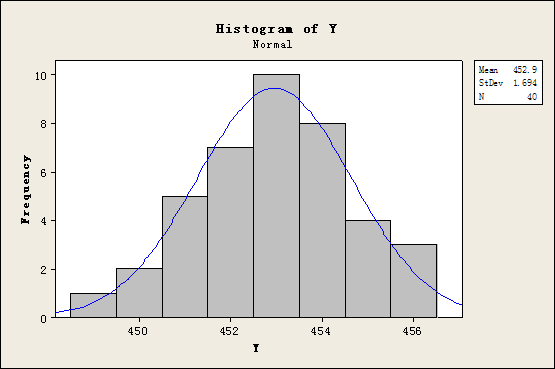
图3 变量Y的直方图

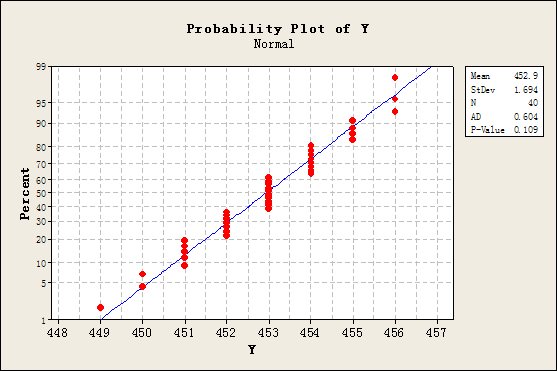
图4 变量Y的正态概率图

由于图4中的P值(P-Value)大于0.05，因而可以认为变量Y服从正态分布。

4.3 相关性检验

变量X、Y之间的散点图如图5所示：

图5 变量X、Y之间的散点图

提出假设：

H₀: ρ=0 ? H₁: ρ≠0

其中，ρ为变量X、Y之间的相关系数。通过统计软件MINITAB关于相关性检验的运算，得到如下输出结果：

由于P值=0.828>0.05，因而接受H₀，即可认为变量X、Y之间线性无关，从而相互独立。

4.4 方差齐性检验

提出假设：

H₀: σ_X=σ_Y ? H₁: σ_X≠σ_Y

其中，σ_X与σ_Y分别为变量X与Y的标准差。通过统计软件MINITAB关于两个总体方差齐性检验的运算，得到如下输出结果与图6：

图6 变量X、Y方差齐性检验

由于P值=0.736>0.05，因而接受H₀，即可认为变量X、Y之间具有相等的方差。

4.5 均值相等检验

提出假设：

H₀: μ_X=μ_Y ? H₁: μ_X≠μ_Y

其中，μ_X与μ_Y分别为变量X与Y的过程均值。通过统计软件MINITAB关于两个总体均值相等检验的运算，得到如下输出结果：

由于P值=0.839>0.05，因而接受H₀，即可认为变量X、Y之间具有相等的均值。

4.6 均值检验

由于两个批次的样本数据独立同分布，故可将它们的数据合并成一个大样本Z，且可认为服从正态分布。两个批次的样本数据几乎都大于或等于标准重量450，因而建立如下假设：

H₀: μ=450 ? H₁: μ>450

其中，μ为数据总体的期望均值。通过统计软件MINITAB关于单总体均值的单边T检验的运算，得到如下结果：

由于P值=0.000<0.05，因而拒绝H₀，即可认为腊肠定量过程的平均重量显著的大于标准重量450。

从上面的计算结果中可以看到，样本数据的均值为452.913，由此再建立如下假设：

H₀: μ=452.913 ? H₁: μ≠452.913

通过统计软件MINITAB关于单总体均值的双边T检验的运算，得到如下结果：

由于P值=0.998>0.05，因而接受H₀，即可认为腊肠定量过程的平均重量为452.913。

4.7 标准差的检验

由于样本数据的标准差为1.63965，因而建立如下假设：

H₀: σ=1.63965 ? H₁: σ≠1.63965

其中，σ为数据总体的标准差。通过统计软件MINITAB关于单个总体方差检验的运算，得到如下输出结果：

从上面的输出结果可以看出，数据总体标准差的95%置信区间为(1.42, 1.94)，该区间包含了样本标准差值1.63965，并且P值=0.958>0.05，因而接受H₀，即可认为腊肠定量过程的标准差为1.63965。

5 改进阶段

5.1 当前过程的最优均值

腊肠的标准重量为450。实际包装过程中，其允许的定量范围为[450, 455]。当检测到腊肠的净重落在该范围之外，则需重新进行定量。由此可知，腊肠净重X是一个连续型随机变量，服从尺度参数σ=1.63965的截尾正态分布。目标值m=450；上下规格限USL和LSL分别为455和450。假定腊肠净重不会低于445，但又不会高于460。

当腊肠净重低于下规格限(445≤X<450)时，此时潜在的损失为退货与换货、法律纠纷以及顾客的流失等，单位产品损失估计值约为0.04元；当腊肠净重高于上规格限(455<X≤460)时，此时损失即为生产成本的增加；当腊肠净重落在规格限内(450≤X≤455)时，此时损失亦为生产成本。由此建立腊肠的损失函数：

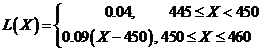(1)

单位产品的检验成本估计值约为0.8元。

因而，单位期望总损失E₁[TC(X)]为：

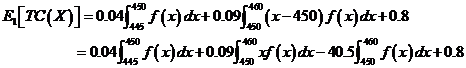(2)

由此建立过程均值优选模型：

(3)

通过MATLAB编程进行迭代计算，得到最优过程均值μ₁*=451.305，单位总质量损失的期望为E₁*(TC)=1.0205。当取μ=m=450时，得到单位总质量损失的期望为E_1m(TC)=1.0584；当取μ=452.913时，得到单位总质量损失的期望为E_1μ(TC)=1.0795。可见，E₁*(TC) < E_1m(TC) < E_1μ(TC)。

5.2 设想过程的最优均值

5.2.1 最优均值及其期望总损失

当前腊肠定量过程所允许的范围为[450, 455]，即大于标准重量450。从另一个角度看，当定量重量略小于标准重量时，顾客满意度的损失一般来说是有限的。当由定量重量的下降所带来的顾客满意度的损失小于由此所带来生产成本的减少，这种定量重量下降对于生产者是有益的。

因而，根据当前腊肠定量的最优过程均值(451.035)略大于标准重量(450)，本文设想腊肠定量过程的取值范围为450±2。由此可以得到，腊肠净重X是一个连续型随机变量，服从尺度参数σ=1.63965的截尾正态分布。目标值m=450；上下规格限USL和LSL分别为448和452。同样假定腊肠净重不会低于445，但又不会高于460。

当腊肠净重低于下规格限(X<448)时，此时潜在的损失为退货与换货、法律纠纷以及顾客的流失等，单位产品损失约为0.04元；当腊肠净重落在下规格限与目标值之间(448≤X≤450)时，此时潜在的损失同样为顾客满意度方面的损失，其损失的度量采用田口式二次损失函数，如式(4)所示：

(4)

当腊肠净重落在目标值与上规格限之间(450<X≤452)时，此时损失即为生产成本；当腊肠净重高于上规格限(X>452)时，此时损失亦为生产成本的增加。由此建立腊肠的损失函数：

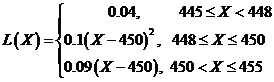
(5)

单位产品的检验成本同样约为0.8元。

因而，单位期望总损失E₂[TC(X)]为：

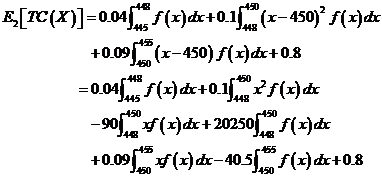(6)

由此建立过程均值优选模型：

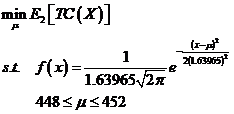(7)

通过MATLAB编程进行迭代计算，得到最优过程均值μ₂*=450.479，单位总质量损失的期望为E₂*(TC)=0.9390元。当取μ=m=450时，得到单位总质量损失的期望为E₂(TC)=0.9447。可见，E₂*(TC) < E_2m(TC) < E₁*(TC)。

5.2.2 灵敏度分析

质量损失系数k=0.1与分布标准差σ=1.64均为估计值，难以准确确定。因而，本文对其进行了灵敏度分析。表2显示了在不同的损失系数和分布标准差下的定量过程最优均值μ*及其单位期望总损失E*(TC)。从该表可以看出，在质量损失系数k不变的情况下，定量过程最优均值μ*随分布标准差σ的增大而增大，其单位期望总损失E*(TC)也随之变大。这是由于随着σ的增大，质量特性值的波动变大，落入规格界限外的概率增大，从而导致期望损失的增大。当分布标准差σ不变时，定量过程最优均值μ*与相应的单位期望总损失E*(TC)随质量损失系数k的增大而增大，但是变化的幅度都非常小，这说明定量过程最优均值μ*对质量损失系数k的变化具有一定的稳健性。

表2 不同的损失系数和分布标准差下的最优特性值

5 控制阶段

将腊肠的定量允许范围从当前的[450, 455]降至[448, 452]，以期降低定量过程的过程均值，从而达到降低单位期望总损失的目的。对今后的腊肠定量过程控制，应依据批次量的大小，设计相应的统计抽样方案，并应用过程控制图监控腊肠净含量值，对任何异常点的出现加以报警。

6 结论

本文采用六西格玛DMAIC流程，对腊肠的包装净含量问题进行研究。首先采集两个不同批次的腊肠，称其净含量，并对其进行统计分析，得到“当前腊肠净含量的期望均值显著的大于标准重量”这一结论；然后通过构造基于质量损失函数与截尾正态分布的极值求解模型，探讨了腊肠定量过程的最优过程均值问题，并设计出较为合理的净含量上下限范围。

[参考文献]

[1] Jiju Antony. Six sigma for service processes [J]. Business Process Management Journal, 2006, 12(2): 234-248.

[2] T.N. Goh, M. Xie. Improving on the six sigma paradigm [J]. The TQM Magazine, 2004, 16(4): 235-240.

[3] Mukhopadhyay A.R., Ray S. Reduction of yarn packing defects using six sigma method: a case stduy [J]. Quality Engineering, 2006, 18(2): 189-206.

[4] Liu E.W. Clinical research of the six sigma way [J]. Journal of the Association for Laboratory Automation, 2006, 11(1): 42-49.

[5] 张斌，王海燕，韩之俊. 基于截尾正态分布的最优过程均值的确定[J]. 数理统计与管理，2008, 27(1): 106-110.

[6] 陈湘来，韩之俊，张斌. 非对称损失函数的质量特性值优化选择[J]. 工业工程，2008, 11(3): 24-26.

[7] 马逢时等．六西格玛管理统计指南[M]．北京：中国人民大学出版社，2007.